My Useless Contribution to the GNU C Sine Function

Have you ever wondered how computers calculate trigonometric functions like sin and cos? Because CPUs can only do basic arithmetic, I always guessed that these functions were implemented using the Taylor Series. I recently decided to dive into the glibc (GNU C Library) source code to verify my theory. While reading the code I noticed some small improvements I could make. This article discusses the changes I merged into glibc and the background knowledge required to understand them.

Taylor Series Review

A Taylor Series lets you approximate any differentiable function as a polynomial. This polynomial approximation becomes increasingly accurate as you include more terms in it. Every Taylor Series also has a center point and the approximation becomes less accurate for values further from the center. All the Taylor approximations in the figure below are centered around 0.

Taylor Series approximations centered at 0 (more terms improve the fit).

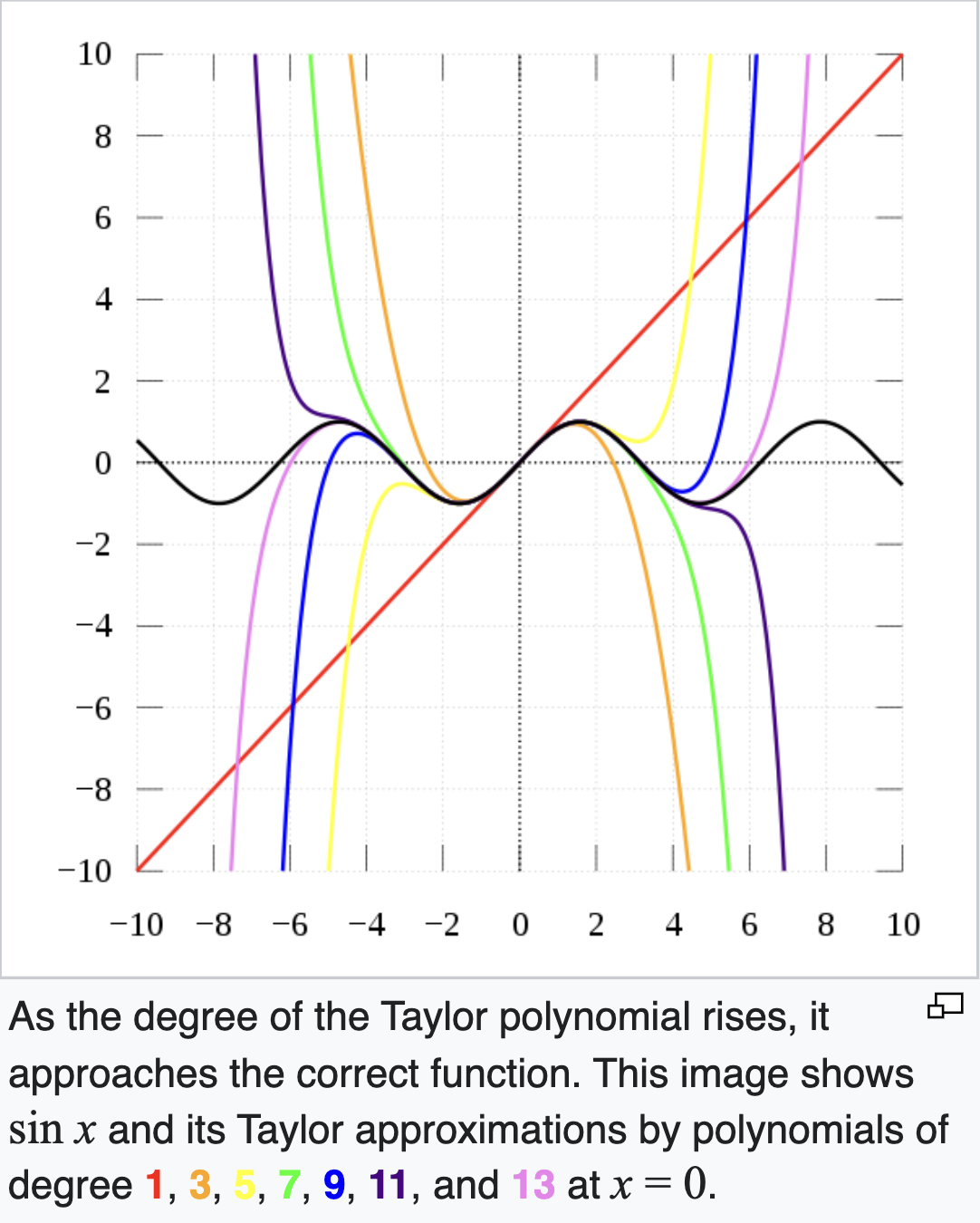
Below is the Taylor Series expansion for a general function f(x) around the center point b, which can be proved via integration-by-parts.

Figure 1:

$$f(x) = f(b) + f'(b)\frac{(x-b)^1}{1!} + f''(b)\frac{(x-b)^2}{2!} + f'''(b)\frac{(x-b)^3}{3!}+\dotsb \newline = \sum_{k=0}^\infty f^{\left(k\right)}(b)\frac{(x-b)^k}{k!}$$

We can use Figure 1 to get the following expansion for the sin function centered around 0.

Figure 2:

$$sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} \dotsb$$

glibc Sine Implementation

If you jump into the s_sin.c file prior to my change, you'll see a comment saying the code implements the following variation of the sin Taylor expansion.

Figure 3:

$$a - \frac{a^3}{3!} + \frac{a^5}{5!} - \frac{a^7}{7!} + \frac{a^9}{9!} + d_a\frac{(1-a^2)}{2}$$

This is exactly what we have in Figure 2, except with the mysterious $d_a\frac{(1-a^2)}{2}$ term at the end. I'll attempt to explain what $d_a$ is and where this last term comes from.

The glibc sine implementation reinterprets its input x as $x=a+d_a$, where $d_a$ is a small number on the order of $10^{-19}$. This technique of expressing one 64-bit value as the sum of two 64-bit values is known as double-double arithmetic. It is a common technique for emulating higher precision when you only have 64-bit primitives to work with. The implementation needs higher precision to combat the rounding errors that compound with each arithmetic operation of the Taylor Series.

Let's verify the last term $d_a\frac{(1-a^2)}{2}$ for ourselves by plugging $a+d_a$ into the formula in Figure 2. We only need to include $d_a$ in the first 2 terms of the expansion because at higher powers the effect of $d_a$ becomes negligible. Because we are calculating the effect of $d_a$ algebraically and then including it at the end, this ensures $d_a$ doesn't get wiped out by later floating point arithmetic.

Figure 4:

$$sin(a+d_a) \approx a+d_a - \frac{(a+d_a)^3}{3!} + \frac{a^5}{5!} - \frac{a^7}{7!} + \frac{a^9}{9!}$$

After expanding via Wolfram Alpha and simplifying we get the relationship below.

Figure 5:

$$sin(a+d_a) \approx a - \frac{a^3}{3!} + \frac{a^5}{5!} - \frac{a^7}{7!} + \frac{a^9}{9!} + (d_a-\frac{a^2d_a}{2}-\frac{ad_a^2}{2}-\frac{d_a^3}{6})$$

We can drop $\frac{ad_a^2}{2}$ and $\frac{d_a^3}{6}$ because they are higher powers of the tiny value $d_a$, so the last term in Figure 5 simplifies to $d_a-\frac{a^2d_a}{2}$. This is different from the term $d_a\frac{(1-a^2)}{2}$ that is included in the comment. If you look at the source code, you'll see the TAYLOR_SIN macro actually computes our version $d_a-\frac{a^2d_a}{2}$ when evaluating the Taylor Series. So it appears the comment isn't correct.

It's also strange how the TAYLOR_SIN macro code below seems to assume a always equals x because it calculates $a^3$ by multiplying xx (which is $x^2$) and a. You can identity the $a^3$ term by looking for which term has the leading coefficient s1, which is the pre-computed value for $-\frac{1}{3!}$. You'll also see that a is indeed equal to x if you check the TAYLOR_SIN macro's only callsite.

/* Helper macros to compute sin of the input values.  */
#define POLYNOMIAL2(xx) ((((s5 * (xx) + s4) * (xx) + s3) * (xx) + s2) * (xx))

#define POLYNOMIAL(xx) (POLYNOMIAL2 (xx) + s1)

/* The computed polynomial is a variation of the Taylor series expansion for
   sin(a):
   a - a^3/3! + a^5/5! - a^7/7! + a^9/9! + (1 - a^2) * da / 2
   The constants s1, s2, s3, etc. are pre-computed values of 1/3!, 1/5! and so
   on.  The result is returned to LHS.  */

#define TAYLOR_SIN(xx, a, da) \
({									                                          \
  double t = ((POLYNOMIAL (xx)  * (a) - 0.5 * (da))  * (xx) + (da));	      \
  double res = (a) + t;							                              \
  res;									                                      \
})

Now that you have seen and understand all the relevant code, here is a summary of the 2 changes I merged into glibc.

1. Update the comment to include the correct last term $d_a-\frac{a^2d_a}{2}$
2. Make it clear that the TAYLOR_SIN macro actually expects x as the second parameter by renaming a → x (and similarly da → dx). Also update the formula in the macro's documentation to reflect this.

I admit these contributions were pointless because neither of them actually introduce a behavior change in the library. But hopefully you learned something by reading this post and find the glibc source code a little more approachable.

Closing Thoughts

After trying to wrap my head around the glibc math library, I have a lot of newfound respect for its creators and maintainers. I wasn't aware that so many advanced numerical computing techniques were needed to accurately compute basic math functions. I'm still surprised that my change was actually accepted by a widely-used core systems library. Working on this was a lot of fun because it required uniting concepts from calculus and computer architecture. I hope to make more open source contributions in the future.

I'd also like to thank Siddhesh Poyarekar and Paul Zimmermann for answering all my glibc questions and reviewing my code.